티스토리 뷰
문제설명은 더보기를 눌러주세요
문제링크 : www.acmicpc.net/problem/20058
마법사 상어는 파이어볼과 토네이도를 조합해 파이어스톰을 시전할 수 있다. 오늘은 파이어스톰을 크기가 2N × 2N인 격자로 나누어진 얼음판에서 연습하려고 한다. 위치 (r, c)는 격자의 r행 c열을 의미하고, A[r][c]는 (r, c)에 있는 얼음의 양을 의미한다. A[r][c]가 0인 경우 얼음이 없는 것이다.
파이어스톰을 시전하려면 시전할 때마다 단계 L을 결정해야 한다. 파이어스톰은 먼저 격자를 2L × 2L 크기의 부분 격자로 나눈다. 그 후, 모든 부분 격자를 시계 방향으로 90도 회전시킨다. 이후 얼음이 있는 칸 3개 또는 그 이상과 인접해있지 않은 칸은 얼음의 양이 1 줄어든다. (r, c)와 인접한 칸은 (r-1, c), (r+1, c), (r, c-1), (r, c+1)이다.
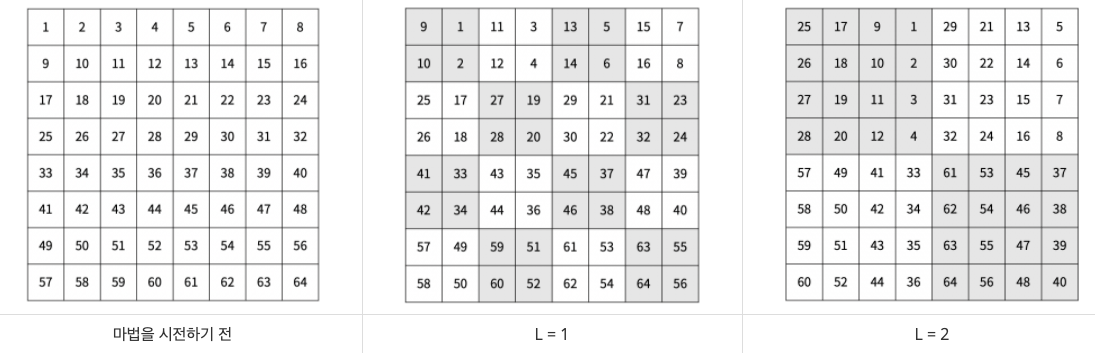
마법사 상어는 파이어스톰을 총 Q번 시전하려고 한다. 모든 파이어스톰을 시전한 후, 다음 2가지를 구해보자.
- 남아있는 얼음 A[r][c]의 합
- 남아있는 얼음 중 가장 큰 덩어리가 차지하는 칸의 개수
얼음이 있는 칸이 얼음이 있는 칸과 인접해 있으면, 두 칸을 연결되어 있다고 한다. 덩어리는 연결된 칸의 집합이다.
입력
첫째 줄에 N과 Q가 주어진다. 둘째 줄부터 2N개의 줄에는 격자의 각 칸에 있는 얼음의 양이 주어진다. r번째 줄에서 c번째 주어지는 정수는 A[r][c] 이다.
마지막 줄에는 마법사 상어가 시전한 단계 L1, L2, ..., LQ가 순서대로 주어진다.
출력
첫째 줄에 남아있는 얼음 A[r][c]의 합을 출력하고, 둘째 줄에 가장 큰 덩어리가 차지하는 칸의 개수를 출력한다.
제한
- 2 ≤ N ≤ 6
- 1 ≤ Q ≤ 1,000
- 0 ≤ A[r][c] ≤ 100
- 0 ≤ Li ≤ N
-풀이-
1. 재귀함수를 통해서 네 부분으로 나눠가며, 한 변의 길이가 2^L과 같아지면 맵을 돌립니다.
2. 돌린 맵을 tempMap에 저장한 후, map에 덮어 씌웁니다.
3. map을 탐색하며, 얼음이 있는 칸 3개 또는 그 이상과 인접해있지 않은 칸의 얼음 양을 1씩 줄입니다.
4. 얼음양이 줄어든 맵을 temp에 저장한 후, map에 덮어 씌웁니다.
5. 파이어스톰을 모두 실행한 후, 남은 얼음양을 계산합니다.
자세한 사항은 주석을 참고해주세요!
-코드-
#include<stdio.h>
#include<algorithm>
#include<cmath>
using namespace std;
void turnMap(int sx, int sy, int ex, int ey);
void DFS(int x, int y, int cnt);
int N, Q, L, map[65][65], temp[65][65], tempMap[65][65], check[65][65];
int ansCnt=0, ans=0, ansA=0;
int dx[] = {-1, 0, 0, 1};
int dy[] = {0, -1, 1, 0};
int main(){
scanf("%d %d", &N, &Q);
N = pow(2, N);
for(int i=1; i<=N; i++){
for(int j=1; j<=N; j++){
check[i][j] = 0;
scanf("%d", &map[i][j]);
}
}
for(int i=1; i<=Q; i++){
scanf("%d", &L);
if(L > 0) turnMap(1, 1, N, N);
for(int i=1; i<=N; i++){ // 얼음 지운 맵을 temp에 저장
for(int j=1; j<=N; j++){
int cnt = 0;
for(int k=0; k<4; k++){
int nx = i + dx[k], ny = j + dy[k];
if(nx < 1 || ny < 1 || nx > N || ny > N || map[nx][ny] == 0) continue;
cnt++;
}
if(map[i][j] == 0) temp[i][j] = 0;
else if(cnt >= 3) temp[i][j] = map[i][j];
else temp[i][j] = map[i][j]-1;
}
}
for(int i=1; i<=N; i++){ // map에 덮어씌우기
for(int j=1; j<=N; j++){
map[i][j] = temp[i][j];
}
}
}
for(int i=1; i<=N; i++){
for(int j=1; j<=N; j++){
if(map[i][j]) ansCnt += map[i][j]; // 얼음의 양
if(map[i][j] && !check[i][j]) { // 얼음의 최대 크기
ansA=0;
check[i][j] = 1;
DFS(i, j, 1);
}
ans = max(ans, ansA);
}
}
printf("%d\n%d", ansCnt, ans);
}
void DFS(int x, int y, int cnt) {
ansA++;
for(int i=0; i<4; i++){
int nx = x+ dx[i], ny = y+ dy[i];
if(nx < 1 || ny < 1 || nx > N || ny > N || map[nx][ny] == 0 || check[nx][ny] == 1) continue;
check[nx][ny] = 1;
DFS(nx, ny, cnt+1);
}
}
void turnMap(int sx, int sy, int ex, int ey){ // 맵 돌리기
int nx = sx+ex-1, ny = sy+ey-1, a = pow(2, L);
if(ex-sx+1 == a && ey-sy+1 == a) { // 변의 길이가 2^L과 같을 때 돌림
int tempMap[65][65];
for(int l=1; l<=L; l++){
for(int i=1+l-1; i<=a-l+1; i++){
for(int j=1+l-1; j<=a-l+1; j++) tempMap[sx+i-1][ey-j+1] = map[sx+j-1][sy+i-1];
for(int j=1+l-1; j<=a-l+1; j++) tempMap[sx+j-1][sy+i-1] = map[ex-i+1][sy+j-1];
for(int j=1+l-1; j<=a-l+1; j++) tempMap[ex-i+1][sy+j-1] = map[ex-j+1][ey-i+1];
for(int j=1+l-1; j<=a-l+1; j++) tempMap[ex-j+1][ey-i+1] = map[sx+i-1][ey-j+1];
}
}
for(int i=sx; i<=ex; i++){ // map에 덮어씌우기
for(int j=sy; j<=ey; j++){
map[i][j] = tempMap[i][j];
}
}
return;
}
turnMap(sx, sy, nx/2, ny/2);
turnMap(nx/2+1, sy, ex, ny/2);
turnMap(sx, ny/2+1, nx/2, ey);
turnMap(nx/2+1, ny/2+1, ex, ey);
}
'PS > 백준' 카테고리의 다른 글
| [C++][백준 1806] 부분합 (0) | 2020.12.15 |
|---|---|
| [C++][백준 2239] 스도쿠 (0) | 2020.12.14 |
| [C++][백준 20057] 마법사 상어와 토네이도 (0) | 2020.10.27 |
| [C++][백준 20055] 컨베이어 벨트 위의 로봇 (0) | 2020.10.20 |
| [C++][백준 20056] 마법사 상어와 파이어볼 (0) | 2020.10.19 |
- Total
- Today
- Yesterday
